Exercícios sobre conjuntos
1. Seja A = { 1, {2}, {1,2} }. Considere as afirmações:
(I) 1 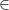 A
A
(II) 2 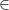 A
A
(III)  A
A
(IV) {1,2} 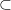 A
A
Estão corretas as afirmações:
A) I e II
B) I e III
C) III e IV
D) III
E) I
2. Sabendo que A = {1, 2, 3, 4}, B = {4, 5, 6} e C = {1, 6, 7, 8, 9}, podemos afirmar que o conjunto (A 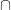 B)
B) 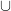 C é:
C é:
A) {1, 4}
B) {1, 4, 6, 7}
C) {1, 4, 5, 6}
D) {1, 4, 6, 7, 8, 9}
3. José Carlos e Marlene são os pais de Valéria. A família quer viajar nas férias de julho. José Carlos conseguiu tirar suas férias na fábrica do dia 2 ao dia 28. Marlene obteve licença no escritório de 5 a 30. As férias de Valéria na escola vão de 1 a 25. Durante quantos dias a família poderá viajar sem faltar as suas obrigações?
A) 19
B) 20
C) 21
D) 22
4.(UNESP) Numa classe de 30 alunos, 16 gostam de Matemática e 20 gostam de História. O número de alunos desta classe que gostam de Matemática e História é:
A) exatamente 16
B) exatamente 10
C) no máximo 6
D) no mínimo 6
E) exatamente 18
5.(PUC) Numa pesquisa de mercado, verificou-se que 15 pessoas utilizam pelo menos um dos produtos A ou B. Sabendo que 10 destas pessoas não usam o produto B e que 2 destas pessoas não usam o produto A, qual é o número de pessoas que utilizam os produtos A e B?
A) 2
B) 3
C) 4
D) 5
Soluções dos Exercícios
A seguir apresentamos as resoluções das questões.
Em questões de conjuntos, é muito comum o uso das palavras “apenas” e “somente”, bem como os conectivos “e” e “ou”, fique atento(a) quanto ao seu uso.
Nesse artigo aqui tem mais dicas sobre o que fazer com relação a tais palavras e mais diversos problemas resolvidos com diagrama de venn.
Exercício 1.
Um ponto importante para chegar a resposta correta desta questão é ter em mente o que é relação de pertinência e sobre a relação entre um subconjunto e conjunto.
A relação de pertinência é usada somente para relacionar o elemento e seu conjunto. Utilizamos para isso o símbolo 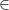 (lê-se: pertence).
(lê-se: pertence).
Para relacionar subconjunto e conjunto, usamos o símbolo 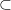 (lê-se: está contido), ou seja, sempre que um conjunto está contido em outro, utilizamos tal símbolo.
(lê-se: está contido), ou seja, sempre que um conjunto está contido em outro, utilizamos tal símbolo.
Claro que o contexto envolvendo a questão deve ser analisado antes, como veremos a seguir na resolução
Analisaremos item por item.
(I) Veja que 1 é elemento de A e o símbolo usado (pertence) para relacionar está correto, então o item I é verdadeiro.
(II) Repare que 2 não é elemento do conjunto A, então ele não pertence a A, logo o item II não está correto. Observe que {2} é elemento de A. Nesse ponto, chamamos a atenção para o fato de que {2} é um conjunto, já que está entre chaves, que é um elemento de A.
Há uma diferença entre 2 e {2}, espero que tenha percebido. O item IV é semelhante.
(III) Uma das propriedades de inclusão (por definição de subconjunto) diz o seguinte: o 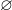 (vazio) está contido em qualquer conjunto. Portanto, o item III está correto.
(vazio) está contido em qualquer conjunto. Portanto, o item III está correto.
(IV) Mais uma vez temos que {1,2} é um elemento de A e não um subconjunto, logo a afirmação não está correta, pois deveria ser usado o símbolo de pertence. Neste caso, o símbolo estaria correto se, ao invés de {1,2} tivéssemos {{1,2}} (subconjunto 1,2).
Temos que somente os itens I e III estão corretos.
Observação: caso você tenha dificuldade para compreender as relações que existem entre um conjunto, elemento e subconjunto estude um pouco mais sobre relação de pertinência e subconjuntos.
Exercício 2.
O exercício pede o conjunto (A 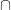 B)
B) 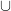 C, “A interseção B união C”.
C, “A interseção B união C”.
Sendo que a relação entre parênteses (interseção) precede a que está fora (união), deve ser realizada antes.
(A 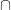 B), o conjunto “A interseção B” é o conjunto formado pelos elementos que pertencem a A e a B, que são comuns aos dois conjuntos.
B), o conjunto “A interseção B” é o conjunto formado pelos elementos que pertencem a A e a B, que são comuns aos dois conjuntos.
A = {1, 2, 3, 4}, B = {4, 5, 6}.
(A 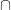 B) = { 4 }.
B) = { 4 }.
Como já obtemos o conjunto “A interseção B”, {4}. Vamos agora realizar a união com C.
O conjunto união (reunião) é formado por todos os elementos que pertencem a um ou a outro conjunto. Todos os elementos dos conjuntos fazem para do conjunto união e não precisa repetir o mesmo elemento.
(A 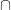 B) = { 4 } e C = {1, 6, 7, 8, 9}.
B) = { 4 } e C = {1, 6, 7, 8, 9}.
(A 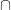 B)
B) 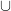 C = {1, 4, 6, 7, 8, 9}.
C = {1, 4, 6, 7, 8, 9}.
Exercício 3.
A resposta para a pergunta deste problema será dada pela interseção dos dias em que cada um poderá faltar sua obrigações. Vejamos:
José Carlos = { 2, 3, 4, 5, …,25, 26, 27, 28 }.
Marlene = { 5, 6, 7, …, 25, 26, 27, 28, 29, 30 }.
Valéria = { 1, 2, 3, 4, 5, …, 25 }
Repare que Marlene só terá licença a partir do dia 5, antes não poderá já que José Carlos e Valéria podem, logo os membros da família só poderão iniciar as férias juntos a partir do dia 5.
Veja que as férias de Valéria terminam no dia 25, logo os membros da família só poderão ficar juntos até dia 25.
Os dias em que a família poderá viajar sem faltar as obrigações vão do dia 5 ao dia 25.
{5, 6, 7, …, 23, 24, 25}, temos um total de 21 dias.
Observação: ao realizar o cálculo da quantidade de dias, tenha atenção para não excluir o dia 5 realizando o seguinte cálculo: 25 – 5 = 20. Deste modo você exclui um dia (5) e está errado já que o dia 5 entra, ok?
Para você calcular a quantidade de números naturais num intervalo dado basta seguir o seguinte método:
(número final) – (número inicial) + 1.
Como exemplo, vamos calcular a quantidade de (dias) números naturais de 5 a 25.
Número final = 25, número inicial = 5.
25 – 5 + 1 = 21.
Exercício 4.
Sejam n(M) e n(H) o número de alunos que gostam de Matemática e História, respectivamente.
n(M U H) = número de alunos que gostam de Matemática ou História (união).
n(M 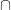 H) = número de alunos que gostam de Matemática e História (interseção).
H) = número de alunos que gostam de Matemática e História (interseção).
Do problema temos: n(M) = 16, n(H) = 20 e n(M U H) = 30.
O número de elementos da união de dois conjuntos finitos (no caso n(M U H)) é dado por:
n(M U H) = n(M) + n(H) – n(M 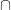 H), fazendo a substituição dos valores.
H), fazendo a substituição dos valores.
30 = 16 + 20 – n(M 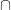 H) <=> n(M
H) <=> n(M 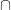 H) = 36 – 30 <=> n(M
H) = 36 – 30 <=> n(M 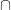 H) = 6.
H) = 6.
Bem, com isso chegamos ao resultado de que o número de alunos que gostam de Matemática e História é igual a 6. Mas, se repararmos nas alternativas, não há esta opção.
E agora?
Ficamos então em dúvida se marcamos a alternativa C) no máximo 6 ou D) no mínimo 6.
Repare o seguinte:
em nossos cálculos acima, consideramos que todos os alunos (30) gostam de pelo menos uma matéria, ok?
Mas, em momento algum o problema diz isso no enunciado, concorda?
Pode haver alunos que não gostam de nenhuma das matérias  e isso aumentaria o número de alunos que gostam de ambas.
e isso aumentaria o número de alunos que gostam de ambas.
 e isso aumentaria o número de alunos que gostam de ambas.
e isso aumentaria o número de alunos que gostam de ambas.
Exemplo: suponha que 1 aluno não goste de Matemática, nem de História.
30 – 1 = 29, isto quer dizer que 29 alunos gostam de Matemática ou História.
Refazendo os cálculos acima para o valor 29, teremos: 36 – 29 = 7 alunos gostam de Matemática e História.
Portanto, o número de alunos que gostam de Matemática ou História deve ser menor ou igual a 30, pois pode haver alunos que não gostam de ambas.
n(M U H) 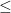 30 <=>
30 <=>
n(M) + n(H) – n(M 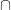 H)
H) 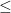 30. Fazendo as substituições.
30. Fazendo as substituições.
16 + 20 – n(M 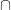 H)
H) 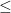 30 <=> 36 – 30
30 <=> 36 – 30 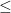 n(M
n(M 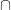 H) <=> 6
H) <=> 6 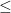 n(M
n(M 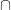 H) ou n(M
H) ou n(M 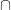 H)
H) 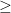 6.
6.
Logo, o número de alunos que gostam de Matemática e História deve ser no mínimo 6.
Exercício 5.
Como 15 pessoas utilizam pelo menos um dos produtos A ou B, temos o seguinte:
10 pessoas não usam o produto B, então elas usam o produto A.
Total de pessoas que usam só A = 10 pessoas.
2 pessoas não usam o produto A, então elas usam o produto B.
Total de pessoas que usam só B = 2 pessoas.
Seja x o número de pessoas que utilizam os produtos A e B (ambos).
Temos que o número de pessoas que usam o produto A, mais o número de pessoas que usam o produto B, mais o número de pessoas que usam ambos deve ser igual a 15 (já que pelo menos um dos produtos é utilizado). Veja:
(nº de pessoas que usam só A) + (nº pessoas que usam só B) + x = 15
10 + 2 + x = 15 <=> x = 3 pessoas.
O número de pessoas que utilizam os produtos A e B é igual 3 pessoas.



Professora boa noite,
ResponderExcluirEu gostaria de saber se a atividade vai ser terminada na sala ou e para concluir em casa.
tathi
Professora boa noite, é a tathi de novo.
ResponderExcluirGostaria de saber se a senhora poderia me ajudar na questão 10 da atividade.
Estou um pouco perdida nesse blog,não sei onde comentar,por isso vou comentar nessa postagem antiga,gostaria que a senhora me ajudasse com uma lista de exercícios de matemática que estou com dúvida,onde posso comentar sobre essa lista?
ResponderExcluirEstou um pouco perdida nesse blog,não sei onde comentar,por isso vou comentar nessa postagem antiga,gostaria que a senhora me ajudasse com uma lista de exercícios de matemática que estou com dúvida,onde posso comentar sobre essa lista?
ResponderExcluir